This program NetCalc is broadly based on
NETCALC - an
RF Impedance Calculator by Ian White, GM3SEK.
NETCALC can be executed on various versions of the Microsoft Windows Operating System.
The L-section code in NetCalc is based on a PERL program by Claude Frantz.
NetCalc is a push-button calculator.
Two versions of NetCalc are currently available.
This version is a Yahoo! Widget which can be downloaded here.
It uses the Yahoo! Widget Engine and runs on Mac OS X and Windows.
There is also a new web widget which can be run in most browsers.
Here is a view of the program when it first opens.
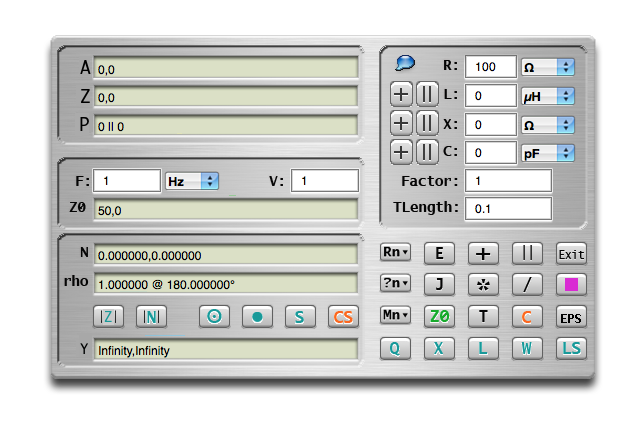
NetCalc displays a number of complex impedance registers, labeled A, Z, P, Z0, N, and rho. The Z and A registers are the first and second elements of a stack.
Note: In Ian White's NETCALC program the first and second elements of the stack are called X and Y.
NetCalc also displays a complex admittance register, labeled Y, which is also used as a general display register.
The impedances each consist of two terms: resistance and reactance. You can do things to the Z impedance alone, or combine the Z and A impedances in various ways.
You have three principal options:
Impedances are entered via the panel at the top right and transfered to the Z register by use of the + and || buttons.
Operations on the Z (and A) register(s) are performed using the buttons at the bottom right. The command names are the same as those in NETCALC, so you should read the NETCALC instructions before attempting to use the program.
The Z and A registers appear in the panel at the top left. The Z register is also shown in parallel form in the P register.
The environment parameters are entered in the middle left panel, apart from Z0 which must first be entered via the impedance input panel and transferred from Z to Z0 using the Z0 button. Complex characteristic impedances can be entered if desired.
Many of the circuit parameters are recomputed at every operation. Others are computed as required.
The panel at the bottom left displays the normalised value of Z in the N register
and the reflection coefficient (in polar form) in the rho register. The normalised admittance is
displayed in the Y register, which is also used as a general display register.
Normalized Impedance = Z/Z0 = R/Z0 + jX/Z0
Normalized Admittance = 1/N = Z0/Z = Z0/(R + jX) = Z0R/(R^2 + X^2) +j(-Z0X)/(R^2 + X^2)
There are buttons to compute the modulus of Z and of N, and four buttons to produce a rudimentary display similar to that on a Smith Chart.
Note: => operator means first operand is pushed onto stack at second operand.
R + L Z => A, R + L -> Z R || L Z => A, R || L -> Z R + X Z => A, R + X -> Z R || X Z => A, R || X -> Z R + C Z => A, R + C -> Z R || C Z => A, R || C -> Z
Rn Z => A, Rn -> Z
E Z <-> A
+ Z + A -> Z, pop(A)
|| Z || A -> Z, pop(A)
?n Rn -> Y
J Z* -> Z
* Z * Factor -> Z
/ Z / Factor -> Z
Mn Z -> Mn
Z0 Z -> Z0
T Z + T(Z0, F, V, length) -> Z
C A -> Z, pop(A)
Q x/r -> Y, where Z = r + jx
Z if x >= 0, L = x/(2πF) -> Y, where Z = r + jx
if x < 0, C = (-2πF)*x -> Y, where Z = r + jx
L L(Z, Z0, F, V) -> Y
W (1 +|rho|)/(1 - |rho|) -> Y,
where rho = ((Z/Z0) - 1)/((Z/Z0) + 1)
LS Displays L-sections matching the load Z to the real part of Z0
|Z| |Z| -> Y |N| |Z/Z0| -> Y
The CIRCLE, POINT, S and CS buttons are used as follows:
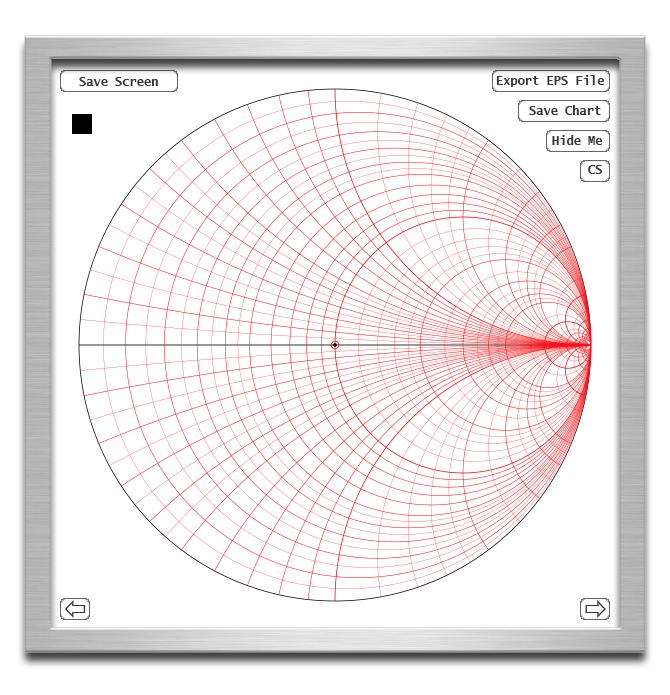
Here is a view of a chart:

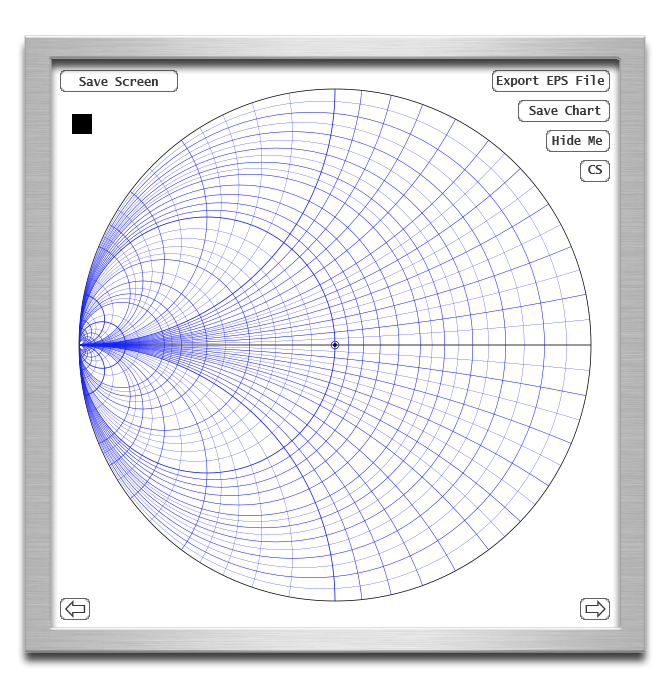
The three available charts are the RX impedance chart (as displayed above),
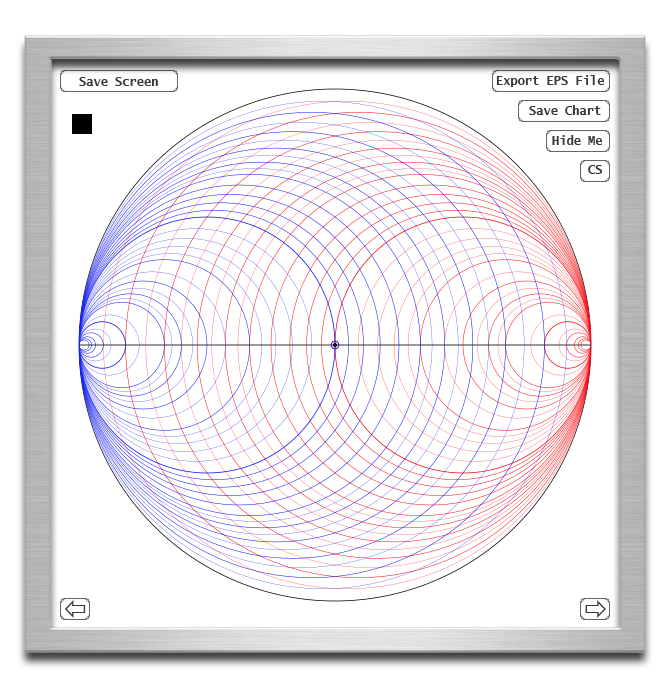
the GB admittance chart and the RG combined chart as displayed below.
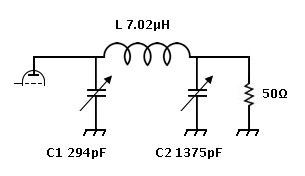
1: Enter 3.75 in the F field - set popup to MHz. 2: Consider C2 in parallel with the 50Ω load: Enter 50 in the R field - set the popup to Ω. Enter 1375 in the C field - set popup to pF. Press || button next to C field.
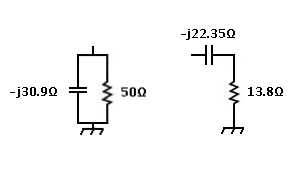
Result is 50.000001 || -30.866413 in the P register,
and 13.796821,-22.349246 in the Z register.
3: Not needed.
4: Consider L in series with the result of step 2:
Enter 0 in the R field
Enter 7.02 in the L field - set the popup to µH.
Press + button next to the L field.
Result is 0.000000,165.404853 in Z the register,
and Infinity || 165.404853 in the P register.
Previous result moves up into the A register.
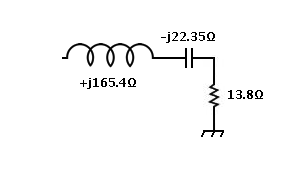
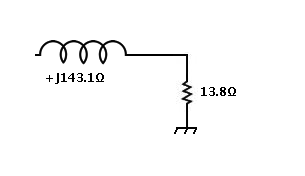
5: Press + button (lower right). Result is 13.796821,143.055607 in the Z register, and 1497.102772 || 144.386224 in the P register
6: Not needed.
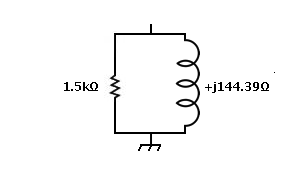
7: Consider C1 in parallel with the result of step 5: Enter 0 in the R field Enter 294 in the C field - set the popup to pF. Press + button next to the C field. Result is 0.000000,-144.358225 in the Z register, and Infinity || -144.358225 in the P register Previous result moves up into the A register.
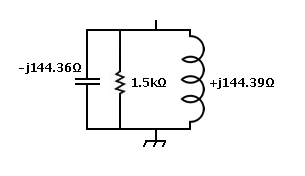
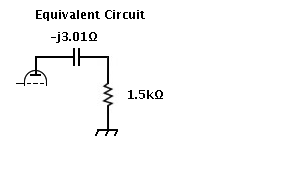
8: Press || button (lower right). Result is 1497.096717,-3.010799 in the Z register, and 1497.102772 || -744422.874115 in the P register Here is the resulting equivalent circuit to the Pi-Tank.
This program is free software; you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation; either version 2 of the License, or (at your option) any later version.
This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
You should have received a copy of the GNU General Public License along with this program; if not, write to the Free Software Foundation, Inc., 51 Franklin St, Fifth Floor, Boston, MA 02110-1301 USA